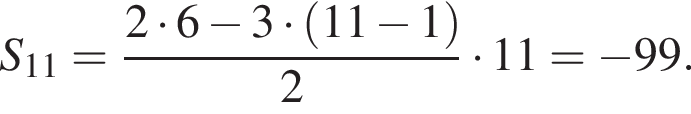Дана арифметическая прогрессия (аn), у которой а9 − а5 = 12, a10 = 14. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения | |
| А) Разность этой прогрессии равна ... Б) Первый член этой прогрессии равен ... В) Сумма первых восьми членов этой прогрессии равна ... | 1) 2 2) −13 3) 4 4) −20 5) 3 |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.

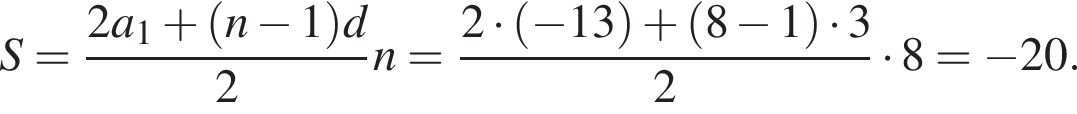
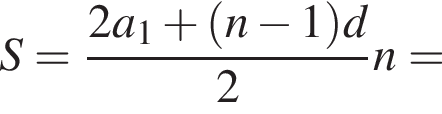
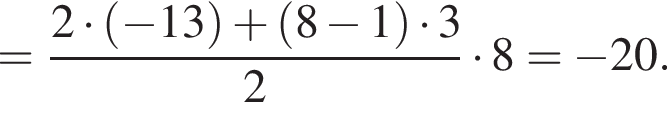
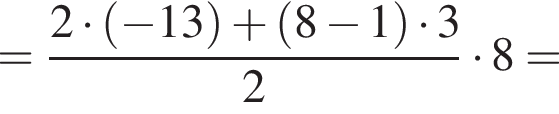
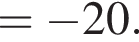
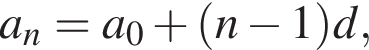 где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 5.
где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 5.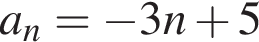
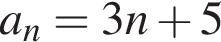
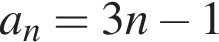

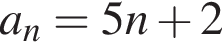
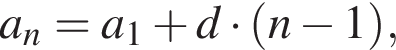 где d — разность арифметической прогрессии. Разность арифметической прогрессии равна
где d — разность арифметической прогрессии. Разность арифметической прогрессии равна  Поэтому
Поэтому 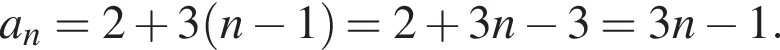
 Известно, что
Известно, что 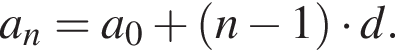 Тогда:
Тогда: 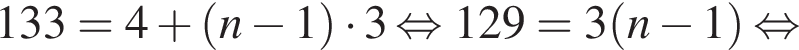
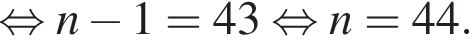
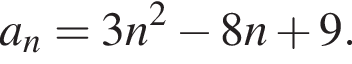 Второй член этой последовательности равен:
Второй член этой последовательности равен: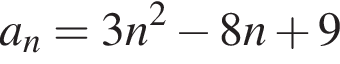 :
: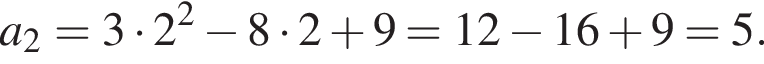
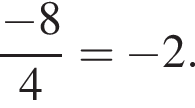
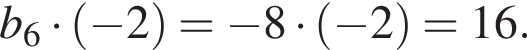
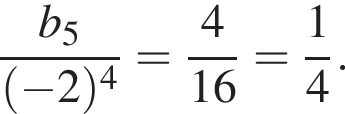
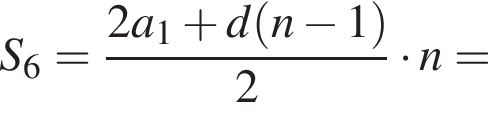
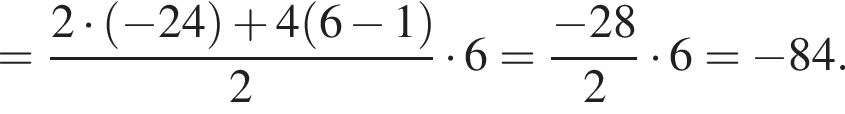
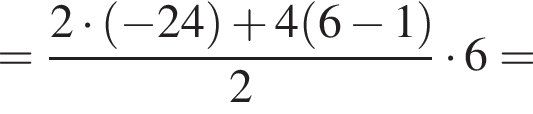
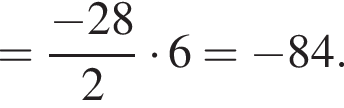
 имеем:
имеем: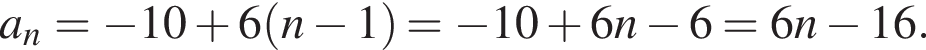
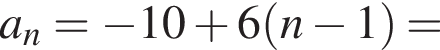

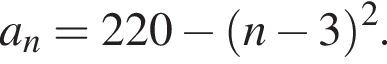 Вычислите
Вычислите 
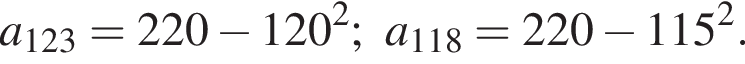 Воспользуемся формулой разности квадратов:
Воспользуемся формулой разности квадратов: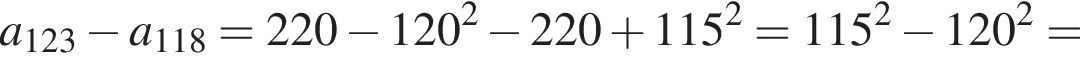
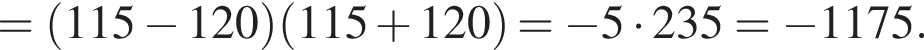
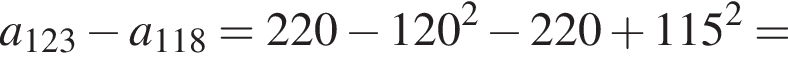
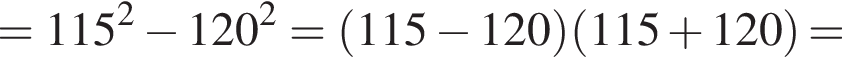
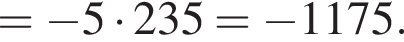
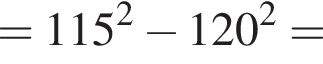
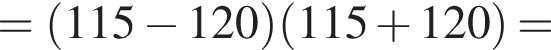
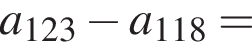
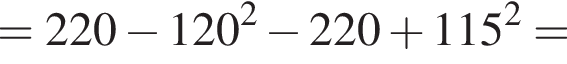
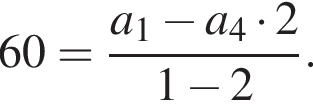 Подставим формулу четвертого члена
Подставим формулу четвертого члена 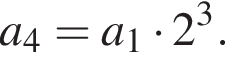 Имеем:
Имеем: 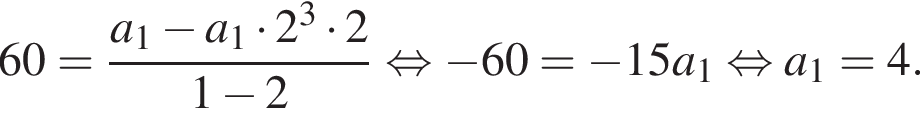
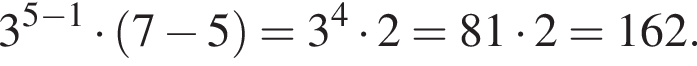
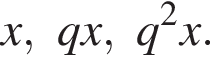
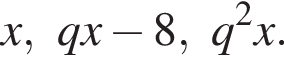
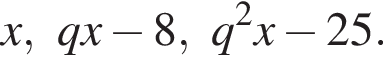
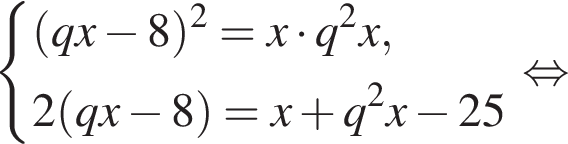
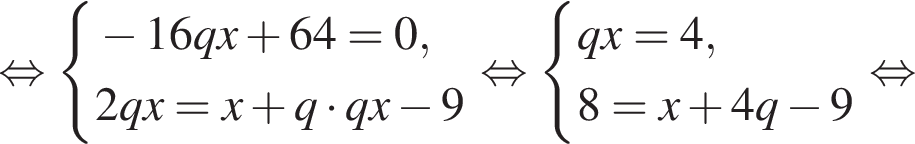
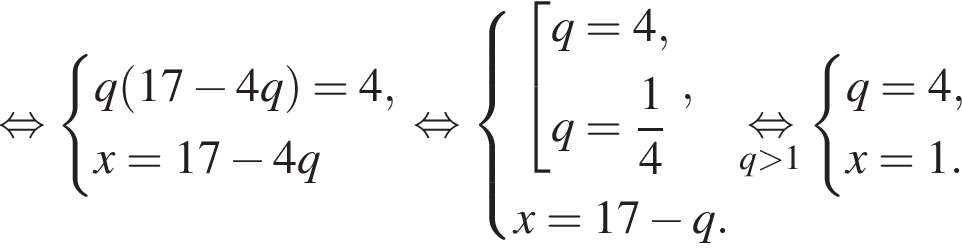
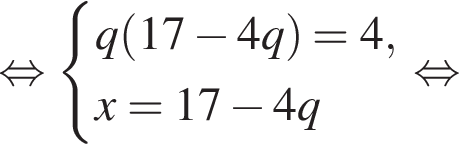
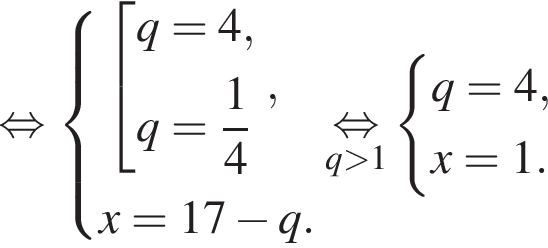
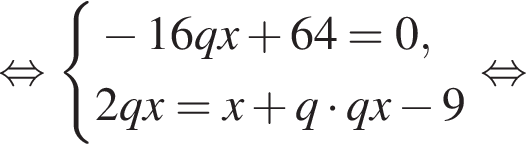
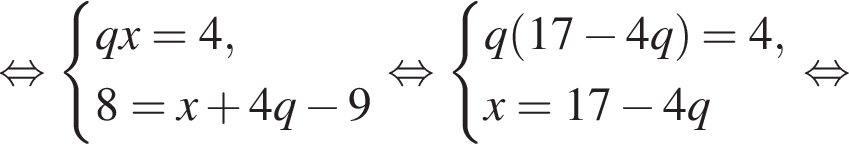
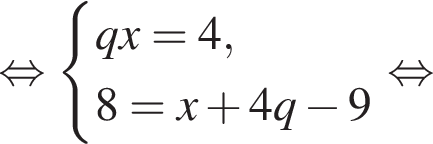
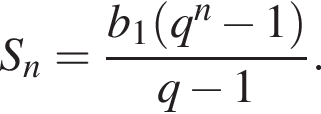 Выразим первый член:
Выразим первый член: 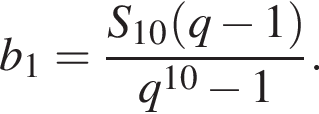 Вспомним, что
Вспомним, что 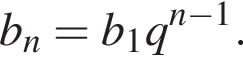
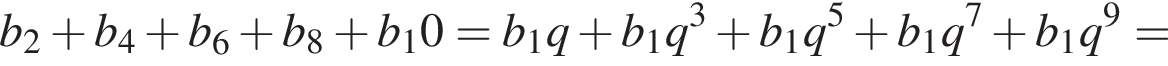
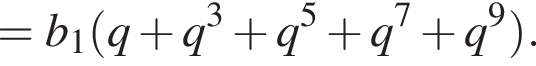
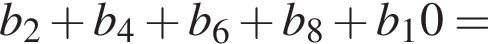
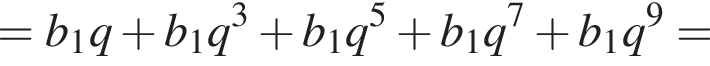
 и знаменателем
и знаменателем 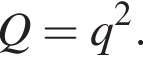 Тогда
Тогда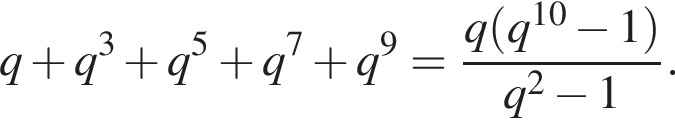
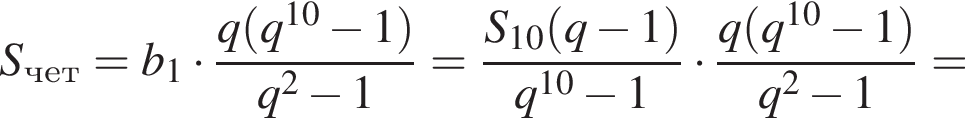
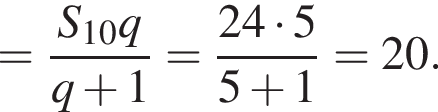
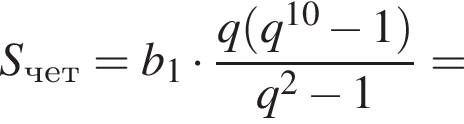
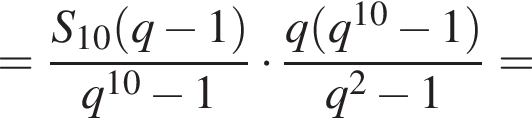
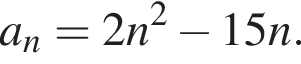 Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.
Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.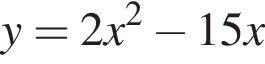 представляет собой параболу ветвями вверх. Поэтому наименьшее значение этой функции достигается при
представляет собой параболу ветвями вверх. Поэтому наименьшее значение этой функции достигается при 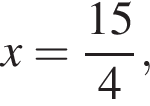 и значения тем больше, чем дальше x от этого числа. Значит, нужно найти ближайшее к
и значения тем больше, чем дальше x от этого числа. Значит, нужно найти ближайшее к 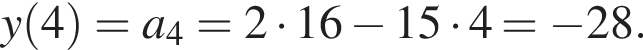 Тогда
Тогда 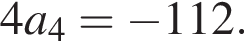
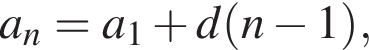 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 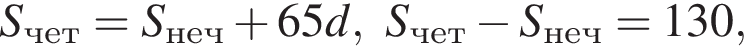 откуда
откуда 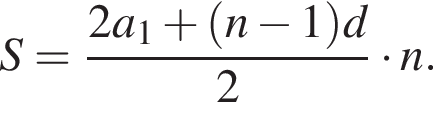 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: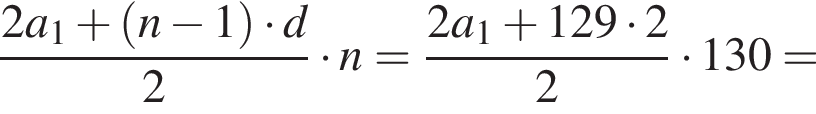
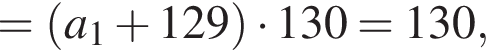
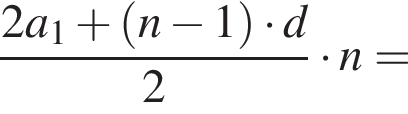
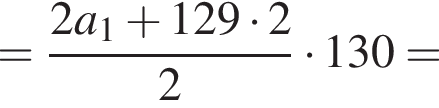
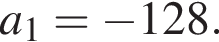 Получим
Получим 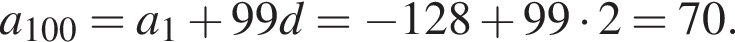
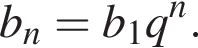
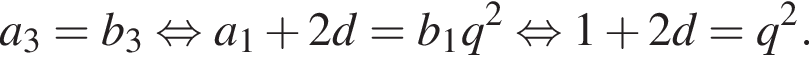
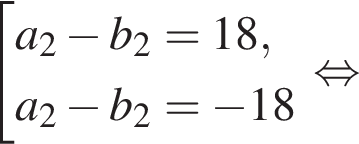
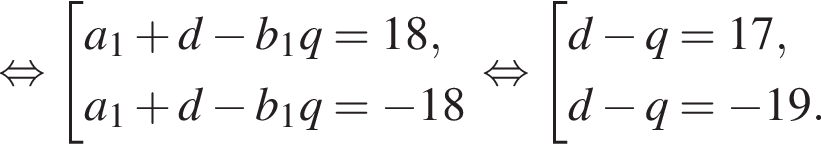
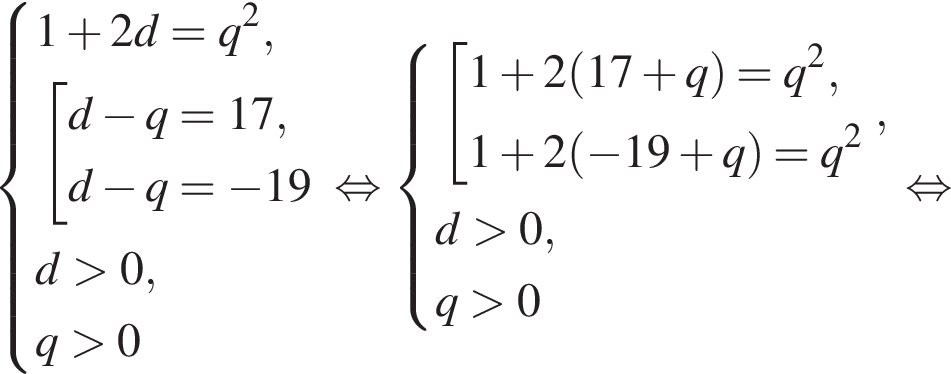
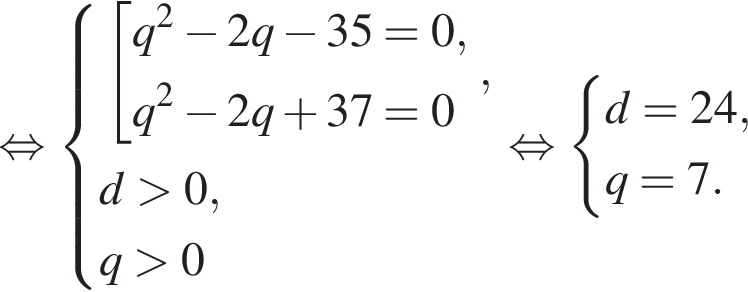
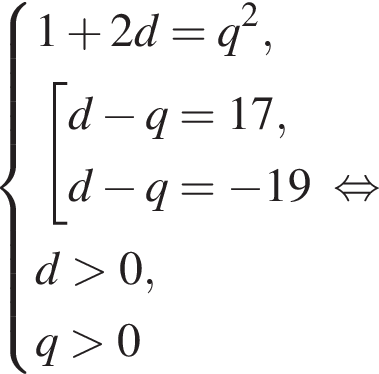
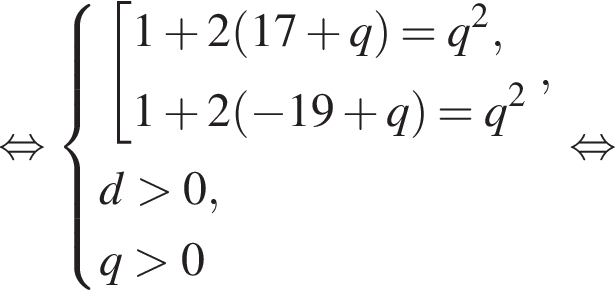
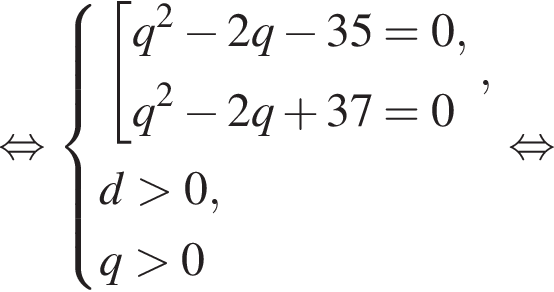
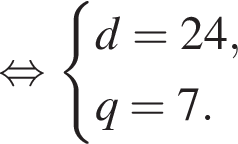
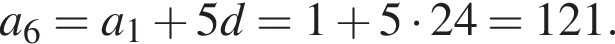
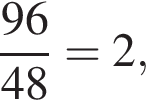 а первый член равен
а первый член равен 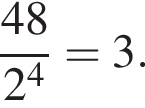 Найдем сумму четырех первых членов геометрической прогрессии:
Найдем сумму четырех первых членов геометрической прогрессии: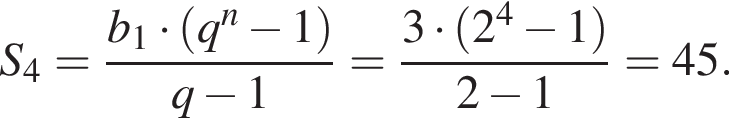
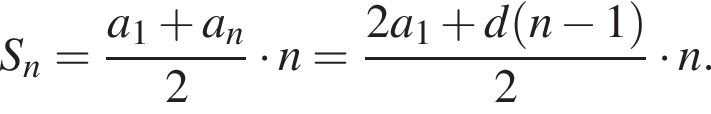
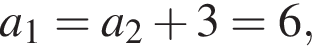 тогда:
тогда: